Patterns In Pascals Triangle - Each frame represents a row in pascal's triangle. Web learn about pascal's triangle, including what it is and how to use it to find coefficients in a binomial expansion in algebra. The next diagonal contains the counting or natural numbers (1, 2, 3,……) the third diagonal contains the triangular numbers (1, 3, 6, 10, 15,……) the fourth diagonal contains tetrahedral numbers (1, 4, 10, 20,……) Web pascal's triangle is an array of numbers that represents a number pattern. Web pascal's triangle is a way to visualize many patterns involving the binomial coefficient. For example, in the 4th row 1 4 6 4 1, sum of the elements is 1 + 4 + 6 + 4 + 1 = 16 = 2 4. Here are some of the ways this can be done: Web pascal's triangle has various patterns within the triangle which were found and explained by pascal himself or were known way before him. To build the triangle, start with 1 at the top, then continue placing numbers below it in a triangular pattern. Expand \((x+y)^4\) using pascal's triangle.
Pascal's Triangle Definition, History, Patterns and its Correlations
To build the triangle, start with 1 at the top, then continue placing numbers below it in a triangular pattern. Each frame represents a row.
Pascal's Triangle Definition, History, Patterns and its Correlations
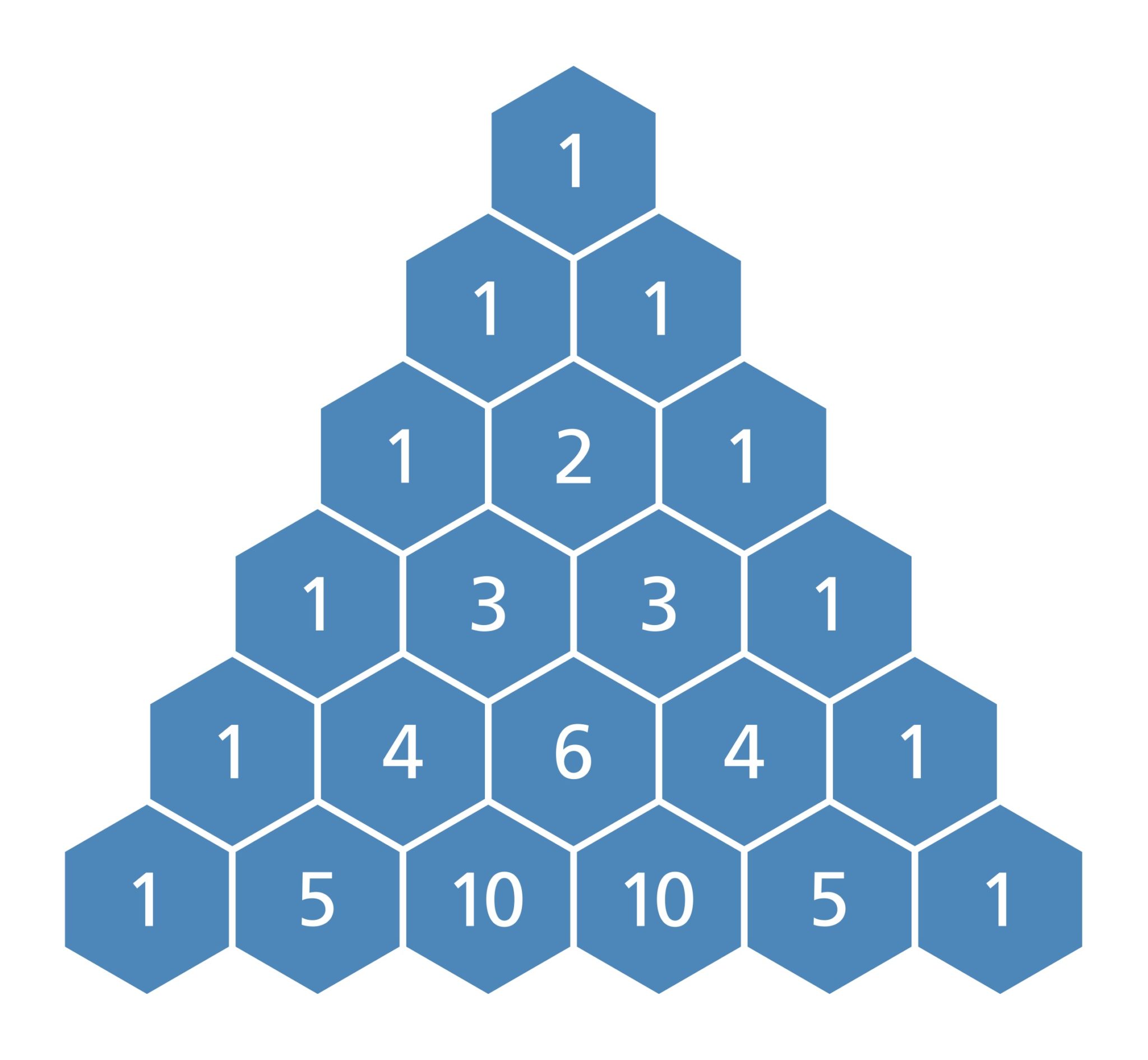
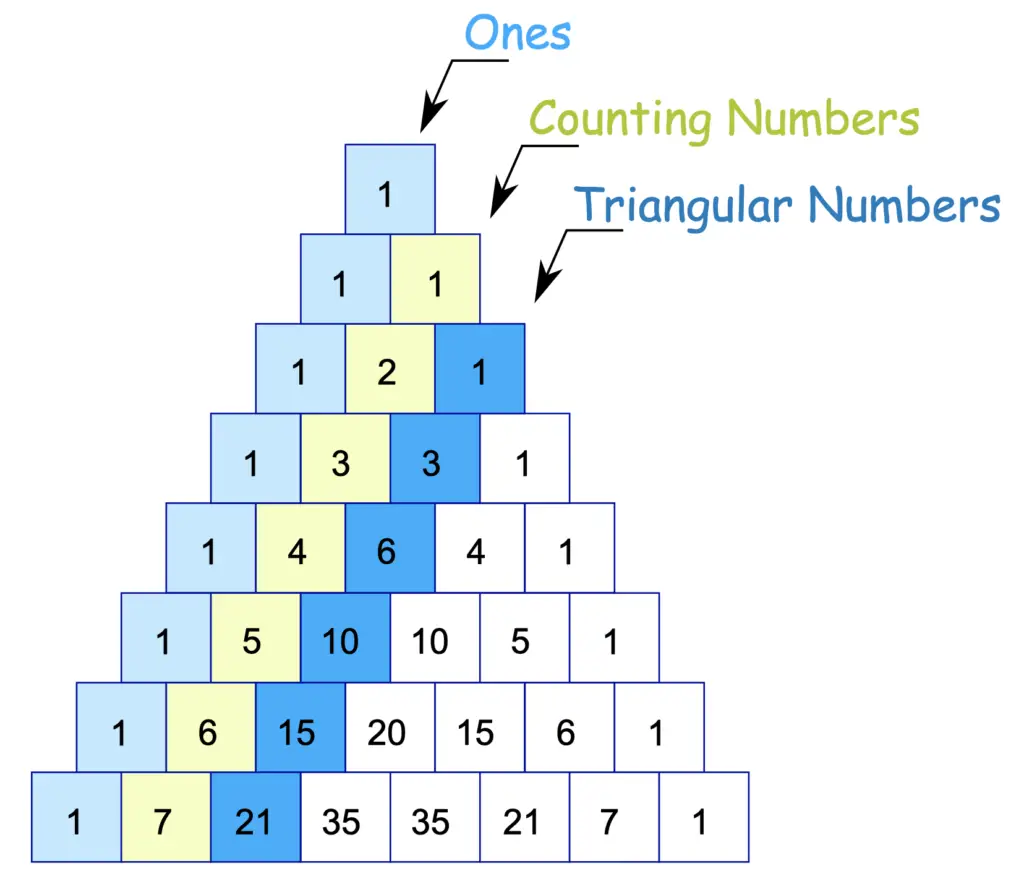
The next diagonal contains the counting or natural numbers (1, 2, 3,……) the third diagonal contains the triangular numbers (1, 3, 6, 10, 15,……) the.
Pascals Triangle Pascals Triangle Pattern With Flowchart And Images
To build the triangle, start with 1 at the top, then continue placing numbers below it in a triangular pattern. Web pascal's triangle has various.
Pascal's Triangle Definition, Formula, Patterns, and Examples
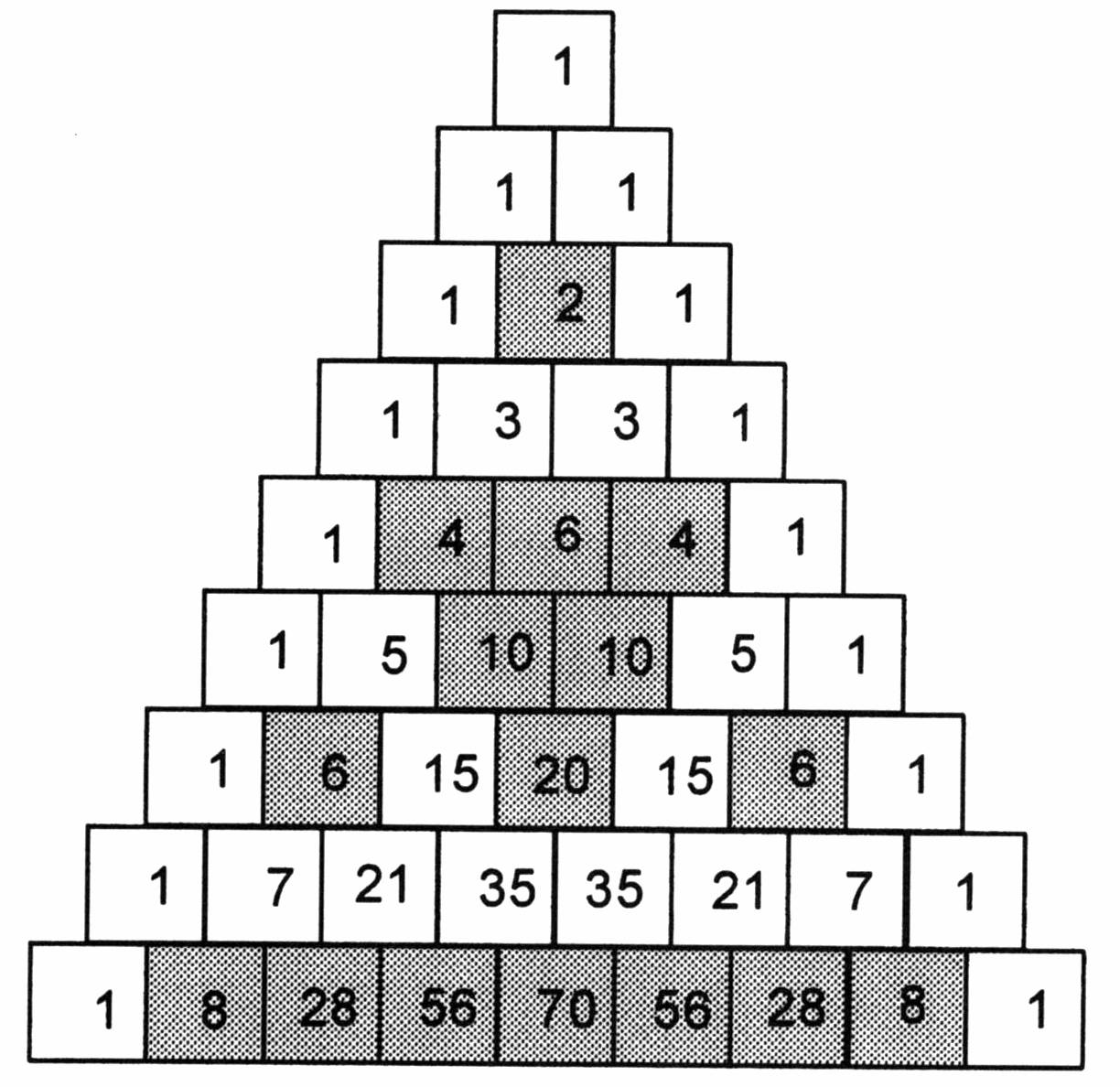
Web pascal's triangle is a way to visualize many patterns involving the binomial coefficient. For example, in the 4th row 1 4 6 4 1,.
Pascal's Triangle (68) YouCubed
In terms of the binomial coefficients, cnm =cnn−m. The next diagonal contains the counting or natural numbers (1, 2, 3,……) the third diagonal contains the.
The Mathematical Tourist Pascal's Patterns
Each frame represents a row in pascal's triangle. Web pascal’s triangle has different patterns within the triangle. Some of them are listed: Web a really.
Interesting Facts About Pascal's Triangle Owlcation
Web learn about pascal's triangle, including what it is and how to use it to find coefficients in a binomial expansion in algebra. Web pascal's.
How to implement the Pascal Triangle in Python practice with loops and
Web pascal's triangle conceals a huge number of various patterns, many discovered by pascal himself and even known before his time. Web pascal’s triangle has.
Pascals Triangle Pascals Triangle Pattern With Flowchart And Images
It has a number of different uses throughout mathematics and statistics, but in the context of polynomials, specifically binomials, it is used for expanding binomials..
Science Visualized • NUMBER PATTERNS PASCAL’S TRIANGLE Pascal’s...
For example, in the 4th row 1 4 6 4 1, sum of the elements is 1 + 4 + 6 + 4 + 1.
Web Pascal's Triangle Conceals A Huge Number Of Various Patterns, Many Discovered By Pascal Himself And Even Known Before His Time.
Web learn about pascal's triangle, including what it is and how to use it to find coefficients in a binomial expansion in algebra. The sum of values in the n th row is 2 n. The first diagonal is ‘1’. The next diagonal contains the counting or natural numbers (1, 2, 3,……) the third diagonal contains the triangular numbers (1, 3, 6, 10, 15,……) the fourth diagonal contains tetrahedral numbers (1, 4, 10, 20,……)
For Example, In The 4Th Row 1 4 6 4 1, Sum Of The Elements Is 1 + 4 + 6 + 4 + 1 = 16 = 2 4.
It has a number of different uses throughout mathematics and statistics, but in the context of polynomials, specifically binomials, it is used for expanding binomials. Web pascal's triangle has many properties and contains many patterns of numbers. Expand \((x+y)^4\) using pascal's triangle. Some of them are listed:
Each Frame Represents A Row In Pascal's Triangle.
To build the triangle, start with 1 at the top, then continue placing numbers below it in a triangular pattern. Web learn about some of the most fascinating patterns in mathematics, from triangle numbers to the fibonacci sequence and pascal’s triangle. In terms of the binomial coefficients, cnm =cnn−m. This interesting pattern and property is named after blaise pascal and has been a famous triangle in mathematics due to its extensive application in.
Web Pascal’s Triangle Has Different Patterns Within The Triangle.
This follows from the formula for the binomial coefficient. Web pascal's triangle has various patterns within the triangle which were found and explained by pascal himself or were known way before him. Here are some of the ways this can be done: The \(n^\text{th}\) row of pascal's triangle contains the coefficients of the expanded polynomial \((x+y)^n\).