Pascals Triangle Patterns - Below is the implementation of the above approach: The second row, or 1 1, gives the coefficients for ( x + y) 1 = x + y; 2.9m views 8 years ago math in real life. For each row, run an internal loop for each element of that row. 1.1^0 is equal to 1. Take time to explore the creations when hexagons are displayed in different colours according to the properties of the numbers they contain. Visit byju's to learn pascal's triangle formula, properties and many solved examples. 1.2 sum of previous values. Web the binomial coefficient formula calculates the number of ways to choose k elements from a set of n elements denoted as “c (n, k)”. Did you guys see this pattern?
Pascal’s Triangle Sophie Drew
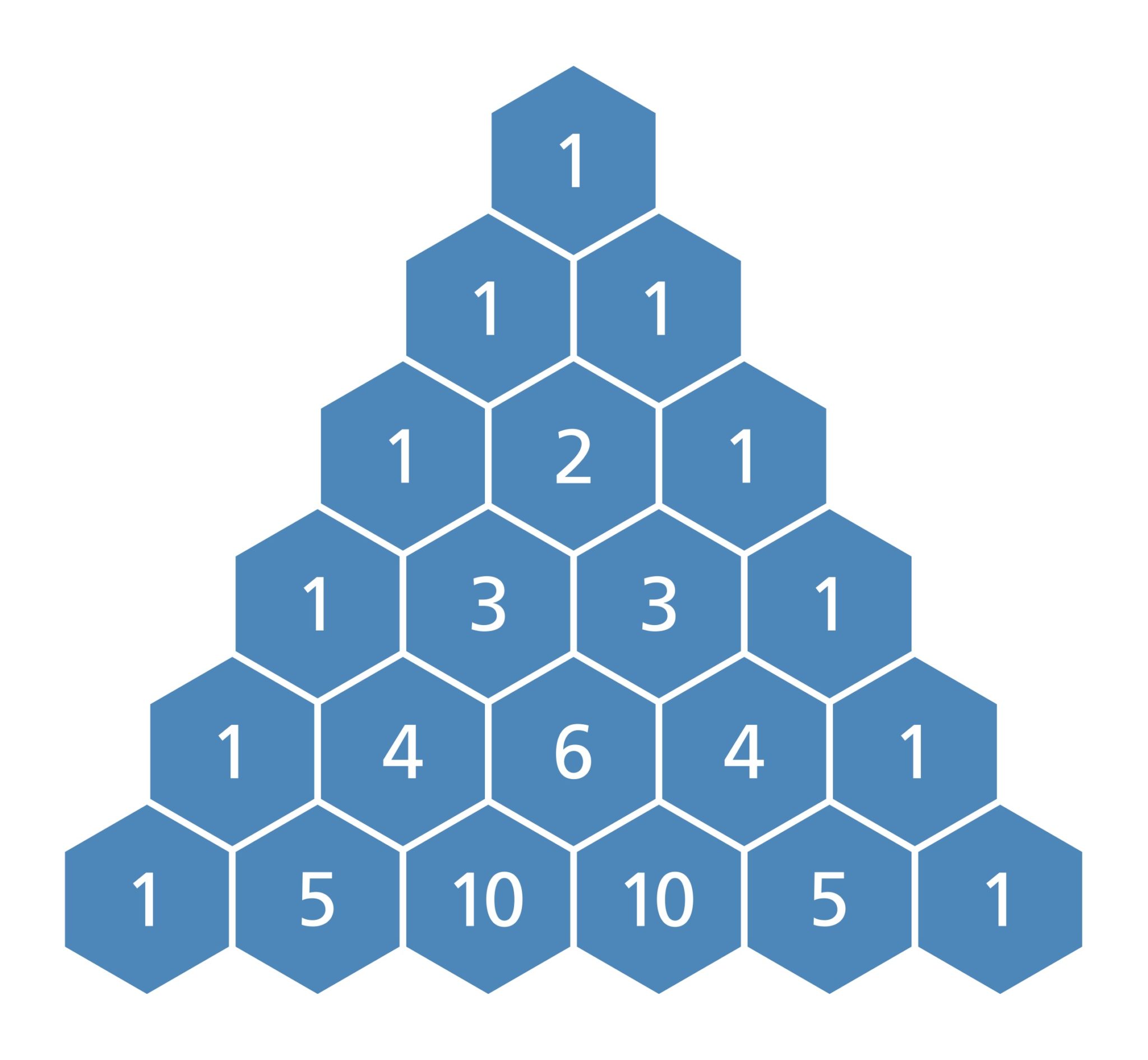
To build the triangle, start with 1 at the top, then continue placing numbers below it in a triangular pattern. Web the binomial coefficient formula.
Pascals Triangle Patterns Browse Patterns
Building pascal's triangle by modified binomial coefficient. 1.6 patterns and properties of the pascal's triangle. 1.1^0 is equal to 1. The simplest pattern is that.
Pascal's Triangle Brilliant Math & Science Wiki
2.9m views 8 years ago math in real life. In terms of the binomial coefficients, cnm =cnn−m. Web pascal's triangle has various patterns within the.
Pascals Triangle Teaching Resources
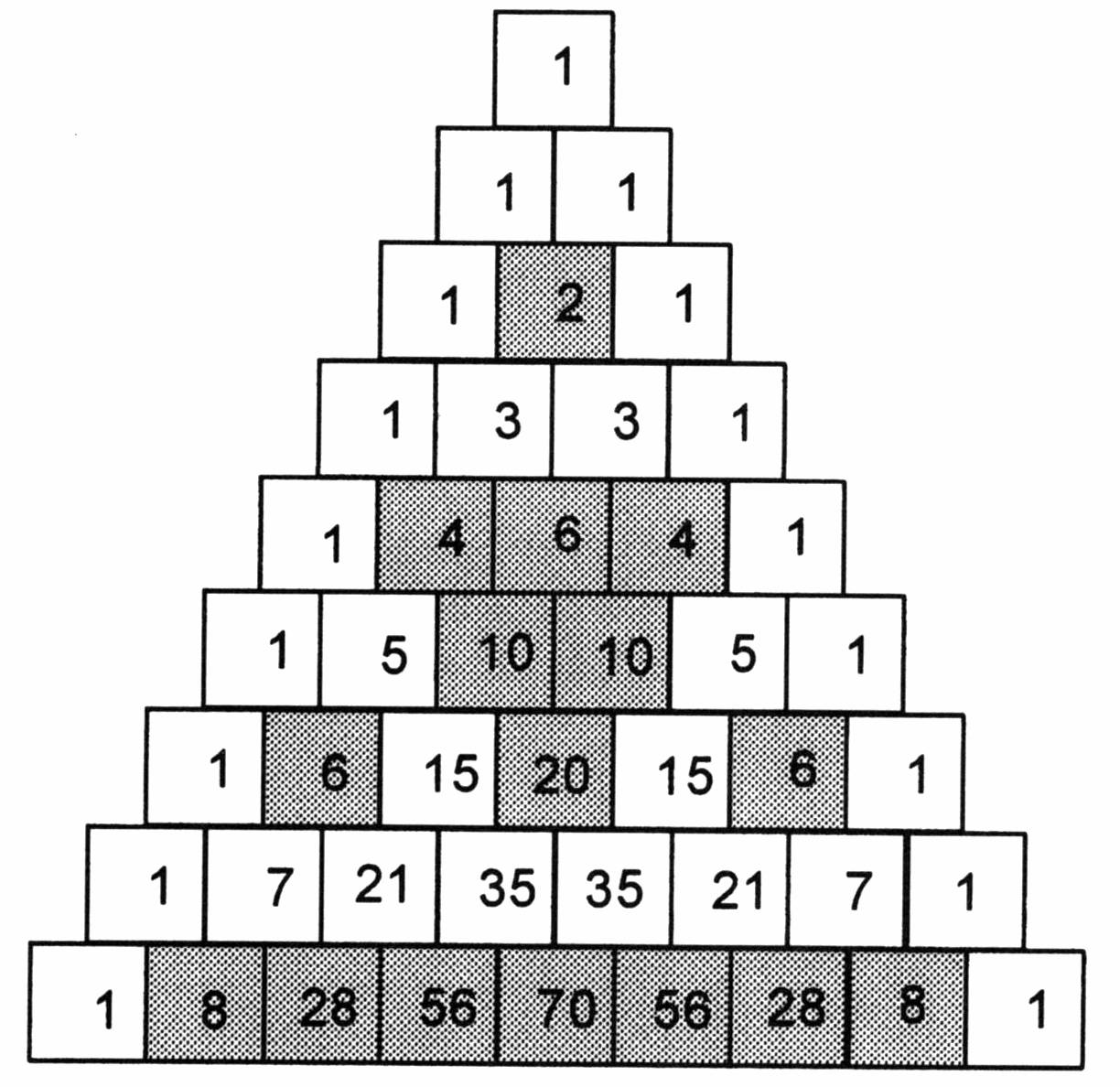
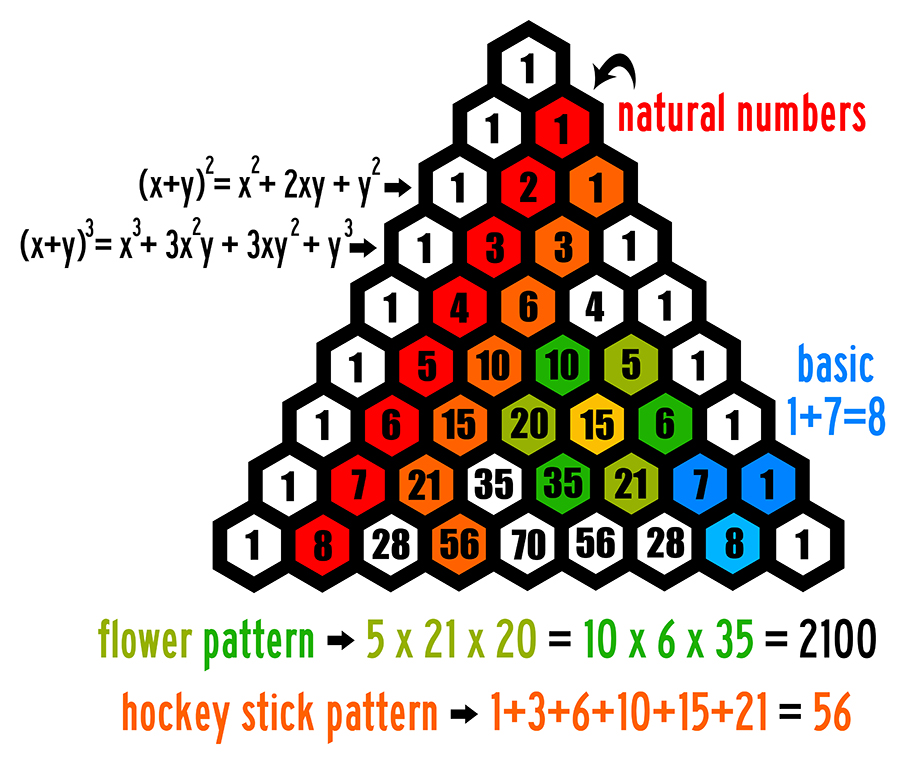
The first diagonal is ‘1’ the next diagonal contains the counting or natural numbers (1, 2, 3,……) the third diagonal contains the triangular numbers (1,.
Pascal's Triangle Definition, Formula, Patterns, and Examples
Web pascal’s triangle is the triangular arrangement of numbers which gives the coefficients in the expansion of any binomial expression. Below you can see a.
Pascal's Triangle Christmas Tree Patterns Math Activity Our Family Code
Take time to explore the creations when hexagons are displayed in different colours according to the properties of the numbers they contain. Building pascal's triangle.
The Mathematical Tourist Pascal's Patterns
The triangle was studied by b. The first diagonal is ‘1’ the next diagonal contains the counting or natural numbers (1, 2, 3,……) the third.
What Is Pascal’s Triangle? Wonderopolis
To build the triangle, start with 1 at the top, then continue placing numbers below it in a triangular pattern. The second row consists of.
Pascal's Triangle (68) YouCubed
Web pascal’s triangle is a number pattern that returns the values or coefficients used in binomial expansions. If i take the number 1.1 and raise.
Pascal's Triangle Definition, History, Patterns and its Correlations
Pascal, in whose posthumous work it appeared in 1665 (pascal 1665). Some of them are listed: It has a number of different uses throughout mathematics.
It Has A Number Of Different Uses Throughout Mathematics And Statistics, But In The Context Of Polynomials, Specifically Binomials, It Is Used For Expanding Binomials.
There are many patterns within pascal's triangle. You can either tick some of the check boxes above or click the individual hexagons. Did you guys see this pattern? Below is the implementation of the above approach:
Run A Loop For Each Row Of Pascal’s Triangle I.e.
(1) where is a binomial coefficient. A few of the pascal triangle patterns are: The second row consists of a one and a one. Some of them are listed:
The Third Row, Or 1 2 1, Gives The Coefficients For ( X + Y) 2 = X2 + 2 Xy + Y2;
Interesting facts about pascal's triangle. If i take the number 1.1 and raise it into those powers, i will get the same results of the pascal's triangle. Expand \((x+y)^4\) using pascal's triangle. These are the first nine rows of pascal's triangle.
1.6 Patterns And Properties Of The Pascal's Triangle.
Web pascal's triangle is a way to visualize many patterns involving the binomial coefficient. The sum of values in the n th row is 2 n. Building pascal's triangle by the previous row. In mathematics, pascal's triangle is a triangular array of the binomial coefficients which play a crucial role in probability theory, combinatorics, and algebra.