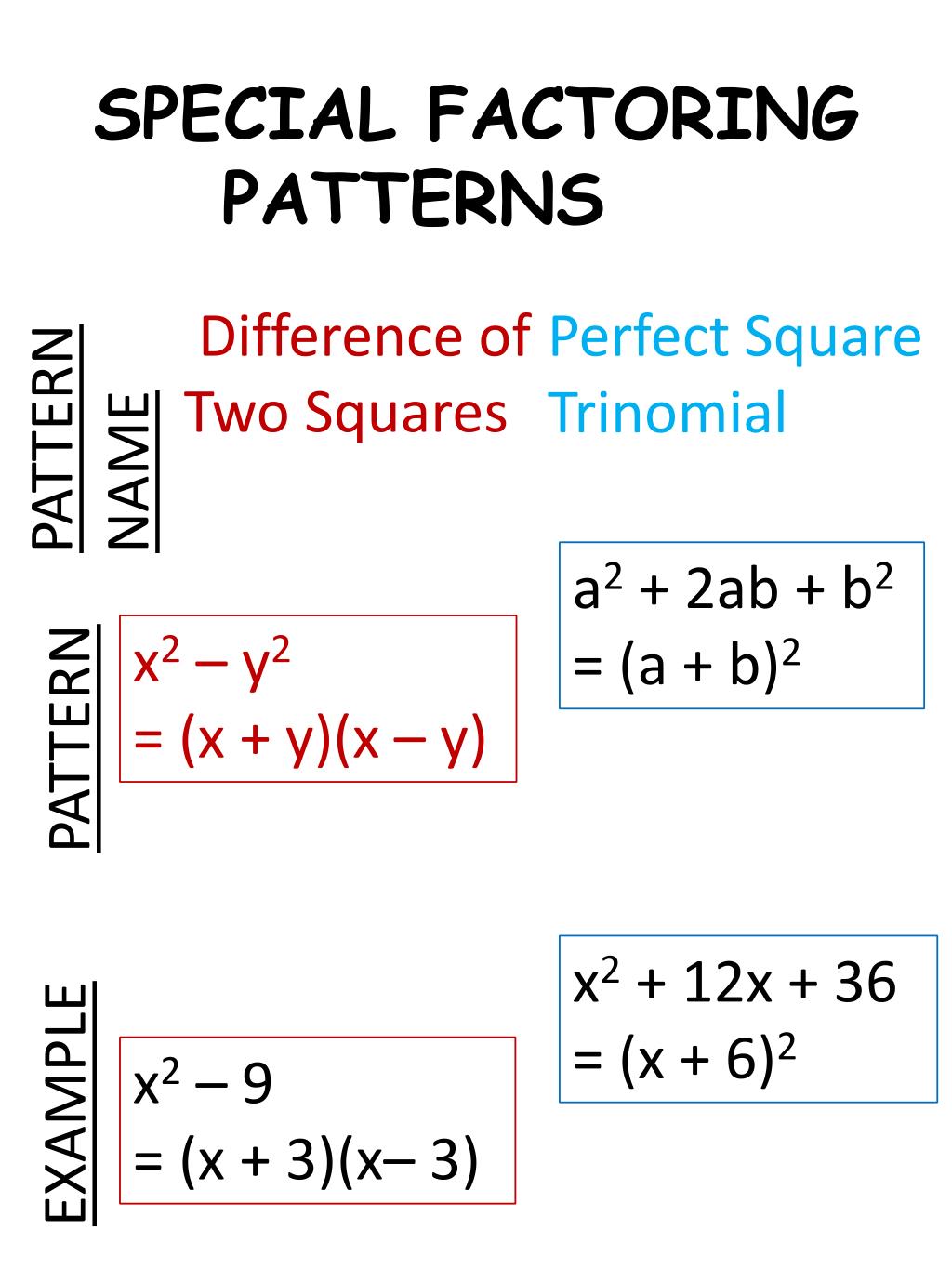
Factoring With Special Patterns - We will write these formulas first and then check them by multiplication. The first and last terms are still positive because we are squaring. (3u2 − 5v2)2 = (3u2)2 − 2(3u2)(5v2) + (5v2)2 = 9u4 − 30u2v2 + 25v4. Web we have seen that some binomials and trinomials result from special products—squaring binomials and multiplying conjugates. 88k views 6 years ago algebra 1. For this quadratic factorization, i need factors of −4 that add up to zero, so i'll use −2 and +2: When factoring there are a few special products that, if we can recognize them, can help us factor polynomials. Web this algebra video focuses on factoring special cases such as different forms of binomials and special products of polynomials specifically perfect square tr. Web example 2 factoring a trinomial of the form ax2 bx c special factoring patterns difference of two squares example a2 b2 (a b)(a b) x2 9 (x 3 )(x 3 ) perfect square trinomial example a2 2ab b2 (a b)2 x2 12x 36 (x 6 )2 a2 2ab b2 (a b)2 x2 8x 16 (x 4 )2 98 algebra 2 notetaking guide • chapter 5 Factoring by sum and difference of cubes.
Ch.11.6 Special Factoring Patterns
Identify and factor special products including a difference of squares, perfect squares, and sum and difference of cubes. If you learn to recognize these kinds.
Algebra 2 Unit 3 Day 5 Factoring Special Patterns and Grouping
Web we have seen that some binomials and trinomials result from special products—squaring binomials and multiplying conjugates. Factoring trinomials using their coefficients. The first and.
Factoring Special Patterns YouTube
The first is one we have seen before. Factoring with the bomb method. Trinomials that are perfect squares, and , which factor as and ,.
Factoring with Special Patterns YouTube
If you learn to recognize these kinds of polynomials, you can use the special products patterns to factor them much more quickly. For this quadratic.
Special factoring patterns YouTube
Factoring with the bomb method. Pull that out of both terms, and write what is left. This is the pattern for the sum and difference.
Factoring Formulas in Algebra What Are Factoring Formulas?
Web example 2 factoring a trinomial of the form ax2 bx c special factoring patterns difference of two squares example a2 b2 (a b)(a b).
Factoring Special Patterns YouTube
Web we have seen that some binomials and trinomials result from special products—squaring binomials and multiplying conjugates. If you learn to recognize these kinds of.
factoring special patterns YouTube
Sometimes, you hardly have to do any work at all to factor a polynomial. X2 − 4 = ( x − 2) ( x +.
How to Factor Polynomials (StepbyStep) — Mashup Math
To expand any binomial, we can apply one of the following patterns. The difference of squares magic, math trick, or math principle, actually works even.
PPT Chapter 6 Section 4 Factoring and Solving Polynomials Equations
Web we have seen that some binomials and trinomials result from special products—squaring binomials and multiplying conjugates. This is the pattern for the sum and.
Factoring With The Bomb Method.
There are some polynomials that, when factored, follow a specific pattern. This is the pattern for the sum and difference of cubes. Factoring trinomials using their coefficients. Web this algebra video focuses on factoring special cases such as different forms of binomials and special products of polynomials specifically perfect square tr.
(X − 3)(X + 3) ( X − 3) ( X + 3).
Learning to identify certain patterns in polynomials helps you factor some “special cases” of polynomials quickly. Web we have seen that some binomials and trinomials result from special products—squaring binomials and multiplying conjugates. Identify and factor special products including a difference of squares, perfect squares, and sum and difference of cubes. Web to factor this, i'll start by writing my parentheses, in the same way as usual for factoring:
Some People Like To Find Patterns In The World Around Them, Like A Game.
[latex] {a}^ {2}+2ab+ {b}^ {2} [/latex] a difference of squares: For this quadratic factorization, i need factors of −4 that add up to zero, so i'll use −2 and +2: (3u2 − 5v2)2 = (3u2)2 − 2(3u2)(5v2) + (5v2)2 = 9u4 − 30u2v2 + 25v4. This reverses the process of squaring a binomial, so you'll want to understand that completely before proceeding.
Factoring By Difference Of Squares.
We have seen that some binomials and trinomials result from special products—squaring binomials and multiplying conjugates. We will write these formulas first and then check them by multiplication. If you learn to recognize these kinds of polynomials, you can use the special products patterns to. Perfect square trinomials of the form: